18P — Solveur de Rubik's Cube
Par admin le lundi, mai 14 2018, 12:00 - 2017-2018 - Lien permanent
Ce projet a été réalisé par Théo ZOMPA.
1. Introduction
Tout le monde a déjà eu en main l’un des plus fameux casse-tête du monde: le Rubik’s cube. Ce casse-tête peut paraître relativement simple à première vue, mais se trouve être en fait redoutablement complexe quand on ne sais pas comment s'y prendre. De ce fait, nombreuses sont les personnes qui n’ont jamais réussi à le résoudre. Mon projet aura pour but de rendre ce casse-tête aussi simple que possible grâce à un programme permettant de résoudre le Rubik’s cube. Le but de mon projet n’est toutefois pas de construire un robot le résolvant tout seul, mais de créer un programme qui nous afficherait les mouvements nécessaires à exécuter afin de le remettre dans sa position originale.
2. Matériel et méthodes
2.1 Matériel
Ce projet demande très peu de matériel. Il nous faudra juste:
- 1x Rubik's cube
- 1x ordinateur avec Python 3.5 et la librairie Numpy
- papier et crayons afin d'aider à visualisation du cube (optionel)
2.2 Méthode
2.2.1Généralité à savoir sur le Rubik's cube
Avant de s'embarquer dans un tel projet, il faut savoir quelques généralités sur le Rubik's cube.
La première et certainement la plus importante, est que les 6 centres du Rubik's cube sont fixes et qu'il ne font rien d'autre que tourner sur eux même. Cela n'a toutefois aucune importance car la couleur restera la même, même si la piece est pivotée à 90 ou 180 degrés. Le fait que ces centres soient fixes nous aide grandement car ils pourront nous servir de repères fixes alors les autres pièces tourneront autours.
Les facettes sont notées sur chaque face de la gauche à droite et de haut en bas. Il y a donc 8 facettes que l'on doit déterminer sur chaque face car celles du centre ne compte pas
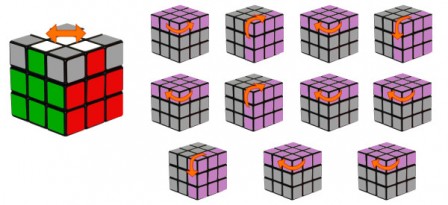
[1]
2.2.2 Installation de Python 3.5 et de Numpy
Tout d'abord il faut installer le programme Python 3.5 qui s'obtient facilement sur cette page web [2]. Une fois Python installé, il faudra importer la librairie Numpy qui nous servira à créer des matrices afin de représenter notre cube. Cette étape est un peu plus difficile et sans la video de "AtoZ Programming Tutorials"[3], je n'y serais certainement jamais arrivé.
2.2.3 Transcrire le cube en 6 matrices
Tout d'abord, il faut réussir à faire parvenir au programme l'état du cube. Pour cela nous allons avoir besoins de 6 matrices 3x3 représentant les 6 faces du cube. Il sera nécessaire pour cela d'aller faire un tour sur le site "Python Numpy Theory" [4] qui m'a permis de comprendre comment écrire des matrices en Python et comment elles interagissaient entre elles. Ne pouvant remplir les matrices qu'avec des variables de type int() ou float(), j'ai eu quelques difficultés à construire des matrices avec le nom des couleurs. J'y suis finalement parvenu en créant des listes, contenant la première lettre de de chaque couleur, que j'ai par la suite mis 3 par 3 sous forme matricielle.
import numpy as np faceU = choixU = str(input('face superieure: ')) while 1: n = 1 i = len(choixU)//n for j in range(i): faceU.append(choixUn*j:n*(j+1)) if len(choixU) != 8: faceU = choixU = str(input('face superieure: ')) else: break
ligne1U = faceU[0,faceU1,faceU2] ligne2U = faceU[3,'W',faceU4] ligne3U = faceU[5,faceU6,faceU7] faceUP = np.array(ligne1U,ligne2U,ligne3U) print('face supérieure: ') print (faceUP)
Ce code nous permettra de choisir la couleur des 8 facettes se situant sur la face blanche dans l'ordre qui suis:

Le code est le même pour déterminer les 6 matrices représentant les 6 faces à l'exception du nom des variables qui sera different ainsi que le nom des matrices.
2.2.4 Créer les mouvements
C'est dans cette étape que les chose se compliquent méchamment... Maintenant que nous avons nos 6 matrices il vas falloir réussir à les faire échanger des données entre elles. Par example lorsque la face du dessus tourne de 90 degrés dans le sens inverse des aiguilles d'une montre, les huit facettes de la face du dessus doivent se réarranger dans le bon ordre tandis que la face avant, la face droite, la face arrière et la face gauche doivent s'échanger 3 facettes.
 (remarquez que les 2 cubes 3x3x3, le 7x7x7x en arrière plan c'est juste pour frimer)
(remarquez que les 2 cubes 3x3x3, le 7x7x7x en arrière plan c'est juste pour frimer)
Si effectuer ce mouvement avec nos deux mains est enfantin, il l'est bien moins lorsque l'on doit le décrire matriciellement sur Python... Il m'a fallut plusieurs heures sur le site SciPy.org[5]pour m'en sortir.
T = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1) S = np.empty_like(T) S1:3,0:12 = T1:3,0:12 S0,0 =T0,9 S0,1 =T0,10 S0,2 =T0,11 S0,3 =T0,0 S0,4 =T0,1 S0,5 =T0,2 S0,6 =T0,3 S0,7 =T0,4 S0,8 =T0,5 S0,9 =T0,6 S0,10 =T0,7 S0,11 =T0,8 T = np.empty_like(S) for i in range(3): Ti, : = Si, : S = np.empty_like(T) Z = np.hsplit(T, 4)
def U(x):
if x < 2:
global faceFRONT,faceDOWN,faceRIGHT,faceBACK,faceLEFT,T,S,Z
faceUP = np.array(ligne1U,ligne2U,ligne3U)
faceFRONT = np.array(ligne1F,ligne2F,ligne3F)
faceRIGHT = np.array(ligne1R,ligne2R,ligne3R)
faceBACK = np.array(ligne1B,ligne2B,ligne3B)
faceLEFT = np.array(ligne1L,ligne2L,ligne3L)
faceDOWN = np.array(ligne1D,ligne2D,ligne3D)
T = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1)
S = np.empty_like(T)
S1:3,0:12 = T1:3,0:12
S0,0 =T0,9
S0,1 =T0,10
S0,2 =T0,11
S0,3 =T0,0
S0,4 =T0,1
S0,5 =T0,2
S0,6 =T0,3
S0,7 =T0,4
S0,8 =T0,5
S0,9 =T0,6
S0,10 =T0,7
S0,11 =T0,8
T = np.empty_like(S)
for i in range(3):
Ti, : = Si, :
S = np.empty_like(T)
Z = np.hsplit(T, 4)
faceUP = np.rot90(faceUP)
print('faceUP:')
print(faceUP)
print('')
faceFRONT = np.array(Z0)
print('faceFRONT:')
print(faceFRONT)
print('')
faceRIGHT = np.array(Z1)
print('faceRIGHT:')
print(faceRIGHT)
print('')
faceBACK = np.array(Z2)
print('faceBACK:')
print(faceBACK)
print('')
faceLEFT = np.array(Z3)
print('faceLEFT:')
print(faceLEFT)
print('')
print('faceDOWN:')
print(faceDOWN)
print('')
else:
faceUP = np.array(ligne1U,ligne2U,ligne3U)
faceFRONT = np.array(Z0)
faceRIGHT = np.array(Z1)
faceBACK = np.array(Z2)
faceLEFT = np.array(Z3)
T = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1)
S = np.empty_like(T)
S1:3,0:12 = T1:3,0:12
S0,0 =T0,9
S0,1 =T0,10
S0,2 =T0,11
S0,3 =T0,0
S0,4 =T0,1
S0,5 =T0,2
S0,6 =T0,3
S0,7 =T0,4
S0,8 =T0,5
S0,9 =T0,6
S0,10 =T0,7
S0,11 =T0,8
T = np.empty_like(S)
for i in range(3):
Ti, : = Si, :
S = np.empty_like(T)
Z = np.hsplit(T, 4)
faceUP = np.rot90(faceUP,x)
print('faceUP:')
print(faceUP)
print('')
faceFRONT = np.array(Z0)
print('faceFRONT:')
print(faceFRONT)
print('')
faceRIGHT = np.array(Z1)
print('faceRIGHT:')
print(faceRIGHT)
print('')
faceBACK = np.array(Z2)
print('faceBACK:')
print(faceBACK)
print('')
faceLEFT = np.array(Z3)
print('faceLEFT:')
print(faceLEFT)
print('')
print('faceDOWN:')
print(faceDOWN)
print('')
C'est une belle et intelligible fonction n'est ce pas ?
Sans aller trop dans les details car je doute que l'assemblage de 4 matrices 3x3 en une matrice 3x12 passionnent beaucoup de monde, le but de cette fonction est d'effectuer ce fameux mouvement du dessus, ou mouvement "U". Afin d'enclencher cette fonction, il faut aller de le shell de Python et taper:
U(1)
pour une rotation de 90 degrés,
U(1) U(2)
pour une rotation de 180 degrés, et
U(1) U(2) U(3)
pour une rotation de 270 degrés. Notons que U(4) reviens à la position de départ car ceci équivaut a une rotation de 360 degrés. Il est va de même avec U(5) qui serait égal à U(1), U(6) qui serait égal à U(2)...etc

La fonction pour le mouvement de la face du bas, le mouvement D, est très similaire a celui du movement U. Seul les matrices faceUP et faceDOWN sont interchangées ainsi qu'une petite partie du code s'occupant du décalage de la matrice (et aussi le nom des variables).
TD = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1) SD = np.empty_like(TD) SD0:2,0:12 = TD0:2,0:12 SD2,0 =TD2,9 SD2,1 =TD2,10 SD2,2 =TD2,11 SD2,3 =TD2,0 SD2,4 =TD2,1 SD2,5 =TD2,2 SD2,6 =TD2,3 SD2,7 =TD2,4 SD2,8 =TD2,5 SD2,9 =TD2,6 SD2,10 =TD2,7 SD2,11 =TD2,8 TD = np.empty_like(SD) for i in range(3): TDi, : = SDi, : SD = np.empty_like(TD) ZD = np.hsplit(TD, 4)
def D(x):
if x < 2:
global faceFRONT,faceUP,faceRIGHT,faceBACK,faceLEFT,TD,SD,ZD
faceUP = np.array(ligne1U,ligne2U,ligne3U)
faceFRONT = np.array(ligne1F,ligne2F,ligne3F)
faceRIGHT = np.array(ligne1R,ligne2R,ligne3R)
faceBACK = np.array(ligne1B,ligne2B,ligne3B)
faceLEFT = np.array(ligne1L,ligne2L,ligne3L)
faceDOWN = np.array(ligne1D,ligne2D,ligne3D)
TD = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1)
SD = np.empty_like(TD)
SD0:2,0:12 = TD0:2,0:12
SD2,0 =TD2,9
SD2,1 =TD2,10
SD2,2 =TD2,11
SD2,3 =TD2,0
SD2,4 =TD2,1
SD2,5 =TD2,2
SD2,6 =TD2,3
SD2,7 =TD2,4
SD2,8 =TD2,5
SD2,9 =TD2,6
SD2,10 =TD2,7
SD2,11 =TD2,8
TD = np.empty_like(SD)
for i in range(3):
TDi, : = SDi, :
SD = np.empty_like(TD)
ZD = np.hsplit(TD, 4)
print('faceUP:')
print(faceUP)
print('')
faceFRONT = np.array(ZD0)
print('faceFRONT:')
print(faceFRONT)
print('')
faceRIGHT = np.array(ZD1)
print('faceRIGHT:')
print(faceRIGHT)
print('')
faceBACK = np.array(ZD2)
print('faceBACK:')
print(faceBACK)
print('')
faceLEFT = np.array(ZD3)
print('faceLEFT:')
print(faceLEFT)
print('')
faceDOWN = np.rot90(faceDOWN)
print('faceDOWN:')
print(faceDOWN)
print('')
else:
faceDOWN = np.array(ligne1D,ligne2D,ligne3D)
faceFRONT = np.array(ZD0)
faceRIGHT = np.array(ZD1)
faceBACK = np.array(ZD2)
faceLEFT = np.array(ZD3)
TD = np.concatenate((faceFRONT,faceRIGHT,faceBACK,faceLEFT),axis=1)
SD = np.empty_like(TD)
SD0:2,0:12 = TD0:2,0:12
SD2,0 =TD2,9
SD2,1 =TD2,10
SD2,2 =TD2,11
SD2,3 =TD2,0
SD2,4 =TD2,1
SD2,5 =TD2,2
SD2,6 =TD2,3
SD2,7 =TD2,4
SD2,8 =TD2,5
SD2,9 =TD2,6
SD2,10 =TD2,7
SD2,11 =TD2,8
TD = np.empty_like(SD)
for i in range(3):
TDi, : = SDi, :
SD = np.empty_like(TD)
ZD = np.hsplit(TD, 4)
print('faceUP:')
print(faceUP)
print('')
faceFRONT = np.array(ZD0)
print('faceFRONT:')
print(faceFRONT)
print('')
faceRIGHT = np.array(ZD1)
print('faceRIGHT:')
print(faceRIGHT)
print('')
faceBACK = np.array(ZD2)
print('faceBACK:')
print(faceBACK)
print('')
faceLEFT = np.array(ZD3)
print('faceLEFT:')
print(faceLEFT)
print('')
faceDOWN = np.rot90(faceDOWN,x)
print('faceDOWN:')
print(faceDOWN)
print('')
Je n'ai toutefois pas créer les fonctions pour les 4 autres mouvements, à savoir F,R,B et L pour des raison de temps et car je n'arrive pas à faire interagir mes fonctions U et D entre elles. En effet je n'ai trouvé aucun moyen pour que les mouvements effectués dans la fonction U soient pris en compte dans la fonction D et vice-versa. J'ai eu les même soucis lorsque j'essayais de coder U2 et U3 car je n'arrivais pas à coder ma fonction de telle sorte qu'elle prenne en compte les mouvements précédents. Il m'a bien fallu 3 heures avant de découvrir la fonction:
global
Cette fontion fait qu'une variable sois la même partout dans une fonction même si elle n'a pas été déclarée dans l'intégralité de cette même fonction. Je ne vois toutefois pas comment utiliser une fonction comme "global" pour lier mes 6 déplacements et je suis donc bloqué à cet endroit
3. Résultats
Je suis bien loin d'avoir réussi mon projet mais j'ai quand même accomplis certaines choses. Premièrement la transcription de l'état du cube se fait facilement, sauf peut-être pour quelqu'un qui n'a jamais touché un Rubik's cube de sa vie. De plus les mouvements U et D fonctionnent parfaitement indépendamment et je suis persuadé qu'il en aurait été de même pour les 4 autres si je les avais codés. Mes ambitions ont été beaucoup trop grandes. Je ne suis même pas arrivé au algorithmes qui auraient permis de résoudre le cube mais je n'y était pas loin. Il m'aurait pour cela fallu trouver comment garder en mémoire les mouvements précédents sur toutes les faces.
4. Discussion
Après quelques heures plongé dans mes matrices je me suis bien rendu compte que ce projet dépassait largement mes connaissances aussi bien informatiques que mathématiques et logiques. Je m'étais donc fixé un nouvel objectif qui était celui de coder tous les mouvement afin de pouvoir simuler un Rubik's cube comme le font des sites comme "Online Rubik'sCube Simulator"[6] mais sans la partie graphique. Ce qui est aussi malheureusement un échec. Mon code fonctionne bien hormis le fait que mes mouvements ne se mélangent pas. Cette erreur ruine du coup toute l'utilité de mon programme mais il est certainement possible de la corriger. Il faudrait pour cela trouver un moyen que les matrices et autres variables ne soient pas que visible à l'intérieur de leur fonction, mais dans l'intégralité du code. J'ai toutefois appris beaucoup de choses en Python durant ce projet, notamment comment coder des fonctions complexes. Il n'était en effet pas simple de manipuler en même temps une dizaine de matrices de tailles différentes et de fonctions différentes, mais je m'en suis finalement sorti.
5. Conclusion
Le but de mon projet qui était de coder un programme permettant de résoudre un Rubis's cube n'a clairement pas été atteint. Mon deuxième but qui était de coder les déplacements des facettes lors des mouvements du cube n'a pas non plus été atteint mais je n'en suis pas loin. Bien que je ne m'y sois pas pris à l'avance pour faire ce projet, je suis content du résultat obtenu. Mon programme n'est pas très impressionnant mais il est relativement complexe si on s'attarde à comprendre comment il fonctionne. Ce projet était bien au delà de mes competences mais je peux m'en prendre qu'à moi car j'aurais du écouter les avertissent de M. Inglesias quant à la difficulté de développer un tel programme. Pour tout ceux qui après avoir lu ce billets sont frustré de ne toujours pas savoir résoudre leur cube, je vous conseille la page "Rubik's cube solver" [7] qui sert à merveille d'exemple à quoi mon projet aurait du ressembler. Je reviendrai certainement sur ce projet une fois mon master de mathématiques en poche mais ce n'est pas encore pour tout de suite. Il me faudra en effet des connaissances dans ce sujet que je ne pourrai certainement qu'acquérir à l'EPFL.
Références
Notes
[1] https://thecube.guru/fr/resolution-rubiks-cube/etape-5/
[2] https://www.python.org/downloads/
[3] https://youtu.be/kTmXHijG8ao
[4] http://cs231n.github.io/python-numpy-tutorial/#numpy
[5] https://docs.scipy.org/doc/numpy-1.14.0/reference/routines.array-manipulation.html
[6] https://ruwix.com/online-puzzle-simulators/
[7] https://rubiks-cube-solver.com